Different types of seismic waves travel at different velocities through any given material. In addition, different materials have different seismic properties, meaning that any one wave type can have a wide range of velocities, depending on the material properties. For instance, the p-wave velocity of shale can range from 800-3,700 m/s. Granite can range from 4,800-6,700 m/s. Because of this, by themselves, seismic velocities alone are not particularly diagnostic with regard to rock type.
Ultimately, seismic velocity depends on the density and elastic properties of the material, whatever its composition. Specifically,
- Compressional-wave velocity depends on the “incompressibility” of the material, as embodied in the bulk modulus. The higher the bulk modulus, the less compressible the material, and the higher the p-wave velocity. Sound travels through water about four times faster than it does through air. Similarly, shear-wave velocity depends on the rigidity of the material, or the resistance to shear. The higher the shear modulus, the higher the s-wave velocity. Mathematically,
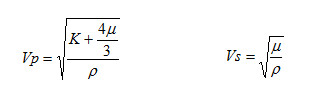
where
K = bulk modulus
µ = shear modulus
ρ = density
Note that Vp depends on both the bulk and shear modulus, while Vs depends only on the shear modulus. This observation implies two things:
- Shear waves always travel slower than compressional waves through a given material.
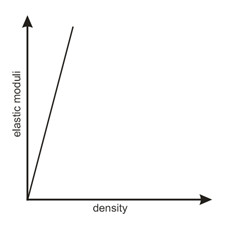
- Materials with zero rigidity – i.e., fluids – do not carry shear waves at all. Therefore, the absence or presence of groundwater has no effect on the shear wave velocity. It is interesting to note that, in general, seismic velocity increases with density – denser rocks tend to be much harder and faster. Yet in the above equations, density is in the denominator. This is known as the “velocity-density paradox”, the answer to which can be found in the fact that the elastic moduli tend to increase with density as well, and at a faster rate.